
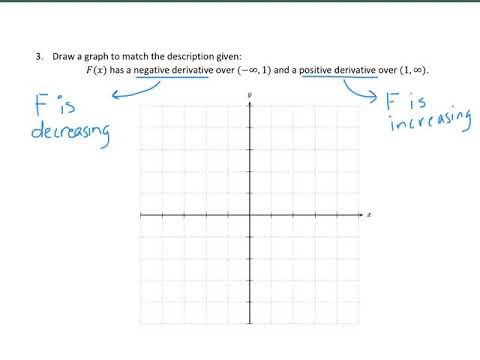
At the maximum (x = 2) and the minimum (x = -2) of f, f ' = 0.Ģ.a - If f ' (a) = 0 or f ' (x) does not exists at x = a and if f ' (x) 0 to the right of a, then f has a relative minimum at x = a.Ģ.b - If f ' (a) = 0 or f ' (x) does not exists at x = a and if f ' (x) > 0 to the left of aĪnd f ' (a) < 0 to the right of a, then f has a relative maximum at x = a.īoth 2.a and 2.b can clearly be verified using the graph in figure 1 above.ģ.b - If f ' (a) has the same sign to the left and to the right of x = a, then f does not have List the x-values in the graph at which the function is not differentiable. The extrema are indicated on the original graph. The original function will either have exactly one local maximum and one local minimum or it will have no extrema. (stationary point) or f ' (a) does not exist.įigure 1: Theorem 1: Function f and its derivativeĪs an example, the graph of f and its derivative f' are shown above. When the first derivative is zero (on the x-axis) and the second derivative is not zero, the original function has local extrema. If function f has a relative minimum or maximum at x = a, we either have f ' (a) = 0 The second derivative of a function is the derivative of the derivative of that function. These are some of the most important theorems in problem solving.
GRAPH BUILDER GIVEN FIRST AND SECOND DERIVATIVE HOW TO
Differentiation and integration constitute the two fundamental operations in single-variable calculus.A tutorial on how to use calculus theorems using first and second derivatives to determine whether a function has a relative maximum or minimum or neither at a given point. The fundamental theorem of calculus relates antidifferentiation with integration. The reverse process is called antidifferentiation.
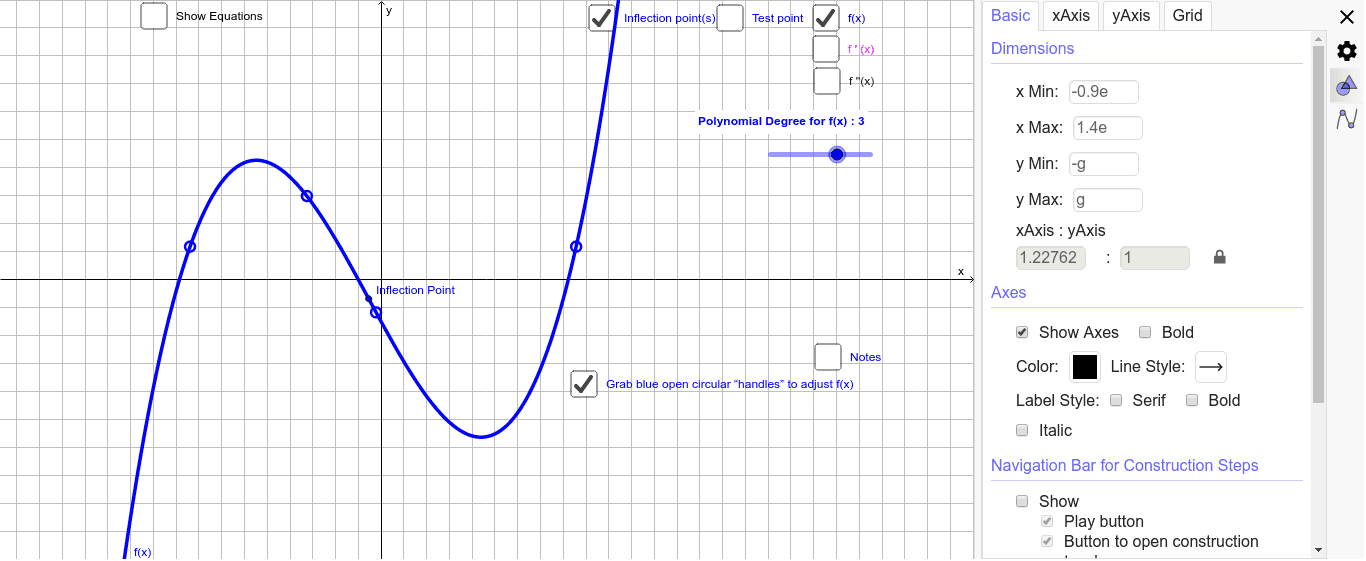
The process of finding a derivative is called differentiation. For a real-valued function of several variables, the Jacobian matrix reduces to the gradient vector. It can be calculated in terms of the partial derivatives with respect to the independent variables. of the second graph, making it more evident that the second lies on top of the first. A function whose second derivative is positive will be concave up (also referred to as convex), meaning that the tangent line will lie below the graph of the function. Figure 10.3.4 shows the graph of this function along with the trace given by. The second derivative of a function f can be used to determine the concavity of the graph of f. Also, for all x, the second derivative is 0. The first two are called unmixed second-order partial derivatives while the. The Jacobian matrix is the matrix that represents this linear transformation with respect to the basis given by the choice of independent and dependent variables. Enter the function as Y1 in the Y 5 menu and the derivative as Y2. For all x, the first derivative f (x) > 0, so the function f(x) is always increasing. In this generalization, the derivative is reinterpreted as a linear transformation whose graph is (after an appropriate translation) the best linear approximation to the graph of the original function. Use first and second derivative theorems to graph function f defined by f(x) x2 Solution to Example 1.step 1: Find the first derivative, any stationary points and the sign of f ' (x) to find intervals where f increases or decreases.f ' (x) 2x The stationary points are solutions to: f ' (x) 2x 0, which gives x 0. This information can be used to draw rough sketches of what a.
For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable.ĭerivatives can be generalized to functions of several real variables. The first derivative can provide very useful information about the behavior of a graph. The tangent line is the best linear approximation of the function near that input value. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. Derivatives are a fundamental tool of calculus. The first derivative test takes only the first derivative of the function, and takes a few points in the neighborhood of the given point, to find if it is the maximum or the minimum point. In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). The first derivative test and the second derivative test are both helpful to find the local minimum and local maximum points.


 0 kommentar(er)
0 kommentar(er)
